Abstract
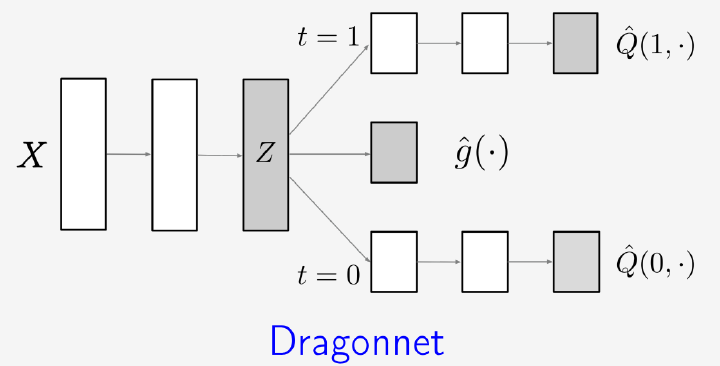
This paper addresses the use of neural networks for the estimation of treatment effects from observational data. Generally, estimation proceeds in two stages. First, we fit models for the expected outcome and the probability of treatment (propensity score) for each unit. Second, we plug these fitted models into a downstream estimator of the effect. Neural networks are a natural choice for the models in the first step. The question we address is how can we adapt the design and training of the neural networks used in the first step in order to improve the quality of the final estimate of the treatment effect? We propose two adaptations based on insights from the statistical literature on the estimation of treatment effects. The first is a new architecture, the Dragonnet, that exploits the sufficiency of the propensity score for estimation adjustment. The second is a regularization procedure, targeted regularization, that induces a bias towards models that have non-parametrically optimal asymptotic properties out-of-the-box. Studies on benchmark datasets for causal inference show these adaptations outperform existing methods.
Reza Rahimi Azghan
Grad Research Associate
I am a Ph.D. student at Arizona State University. I work as a Graduate Research Associate at Embedded Machine Intelligence Lab (EMIL) under the supervision of Dr. Hassan Ghasemzadeh.